ciespec2wp

The ciespec2wp function determines the white point of an illuminant’s spectral power distribution. Any errors in the data set or in results generated with the Lighting Toolbox are not in the liability of the CIE nor me, see licence.

See also: ciewhitepoint

Usage:

[XYZ,xyz] = ciespec2wp(lam,spec,observer)

Where:

Examples

Whitepoint of CIE standard illuminant ‘A’, ‘E’ and ‘D65’:

lam = 360:830;
spec = ciespec(lam,{'A','E','D65'});
[XYZ,xyz] = ciespec2wp(lam,spec)

See also: ciewhitepoint, ciespec

Result:

XYZ =

   1.0984   1.0000   0.3559
   1.0001   1.0000   1.0003
   0.9505   1.0000   1.0888

xyz =

   0.4475   0.4074   0.1450
   0.3333   0.3333   0.3334
   0.3127   0.3290   0.3582

Whitepoint of CIE standard illuminant ‘A’ for 10° standard observer:

lam = 360:830;
spec = ciespec(lam,'A');
[XYZ,xyz] = ciespec2wp(lam,spec,'xyz10')

See also: ciewhitepoint, ciespec

Result:

XYZ =

   1.1114   1.0000   0.3521

xyz =

   0.4511   0.4059   0.1429

Determine the tristimulus values X,Y,Z for standard illuminant ‘D65’ with an resulting photometric value of Y = 15000:

lam = 360:830;
spec = ciespec(lam,'D65');
XYZ = ciespec2wp(lam,spec).*15000

See also: ciewhitepoint, ciespec

Result:

XYZ =

   1.4257e+04   1.5000e+04   1.6332e+04

Determine and plot the whitepoint of an artificial spectral power distribution (SPD):

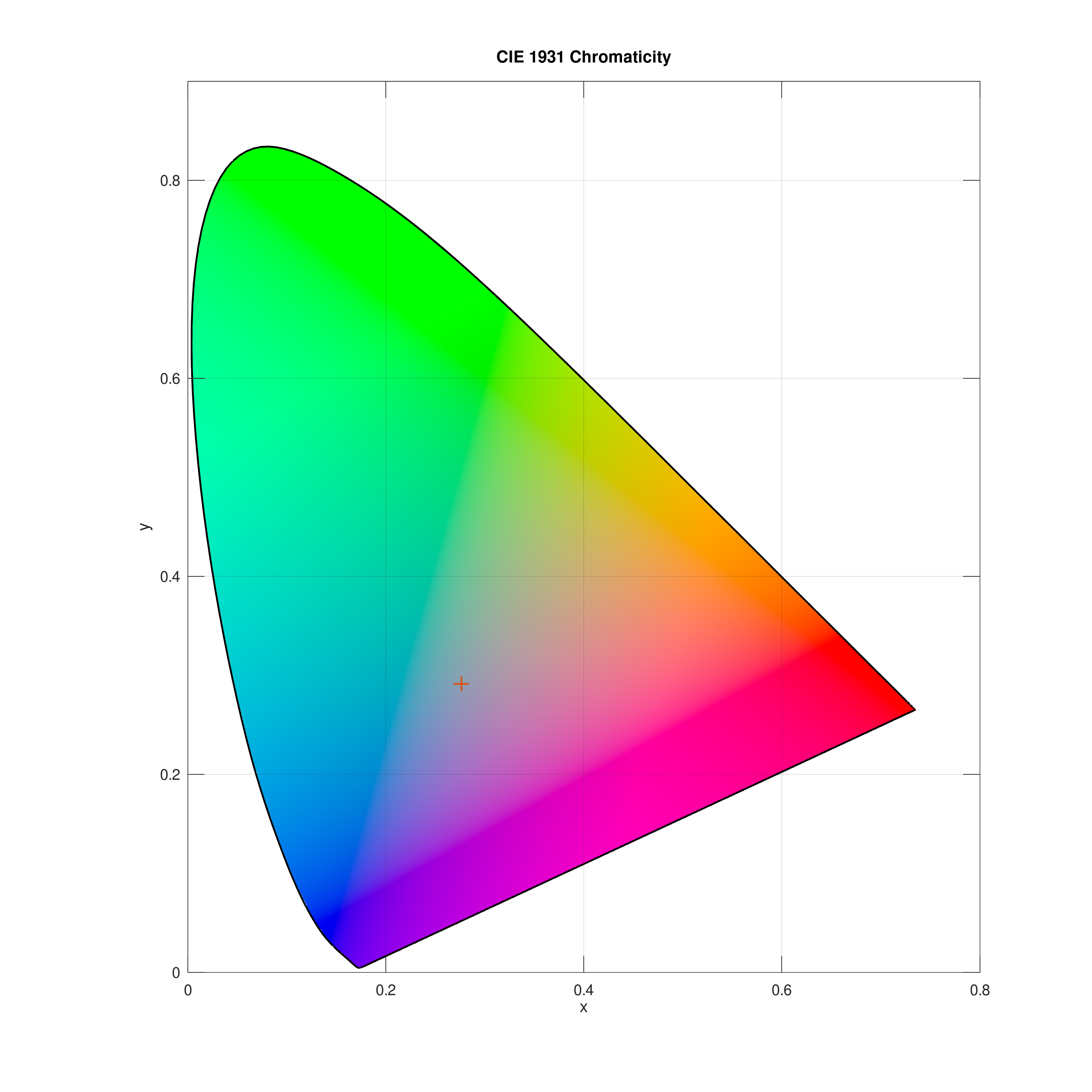
lam = 380:780;
% create a linear decreasing SPD
spec = linspace(1,0,numel(lam));
[~,xyz] = ciespec2wp(lam,spec)
plotciexy(xyz(1),xyz(2))

See also: plotciexy

Result:

xyz =

   0.2762   0.2916   0.4322

References: