planck
The planck function calculates the spectral radiant exitance M of a Planck radiator for a given black body temperature T in K, as in equation 1:
(1) \qquad M(\lambda,T) = \frac{c_1}{\lambda^5}\frac{1}{\exp\left({\frac{c_2}{T\cdot\lambda}}\right)-1}
With:
c_1 = 3.741771852 \cdot 10^{-16}~\mathrm{W}\cdot\textrm{m}^2 c_2 = 1.438776877 \cdot 10^{-2}~\mathrm{m}\cdot\textrm{K}Note: Since the redefinition of the Boltzmann constant in 2018 the constants c_1 and c_2 are now exact values.
Usage:
[M,x,y,u,v] = planck(T,lam,mode)
Where:
| Parameter | Description |
M | Is the planck radiator’s spectral radiant exitance in \textrm{W} \textrm{m}^{-2} \textrm{nm}^{-1}. |
x,y | Are the colour coordinates in CIE 1931 chromaticity of M. |
u,v | Are the colour coordinates in CIE 1960 chromaticity of M. |
T | Is the planck radiator’s temperature in K. |
lam(optional) | Specifies the wavelengths in nm, default: 360:830 |
mode | Specifies the constants c_1 and c_2: ‘exact’ using the exact values as from NIST \qquad c_1 = 3.741771852 \cdot 10^{-16}~\mathrm{W}\cdot\textrm{m}^2 \qquad c_2 = 1.438776877 \cdot 10^{-2}~\mathrm{m}\cdot\textrm{K} ‘CIE’ using the values specified by the CIE e.g. in CIE TR 224 \qquad c_1 = 3.74183 \cdot 10^{-16}~\mathrm{W}\cdot\textrm{m}^2 \qquad c_2 = 1.4388 \cdot 10^{-2}~\mathrm{m}\cdot\textrm{K} |
Examples
Spectral radiant exitance for a block body temperature of 5000 K:
M = planck(5000);
plotspec(360:830,M)
ylabel('spectral radiant exitance in W m^{-2} nm^{-1}')
See also: plotspec
Result:
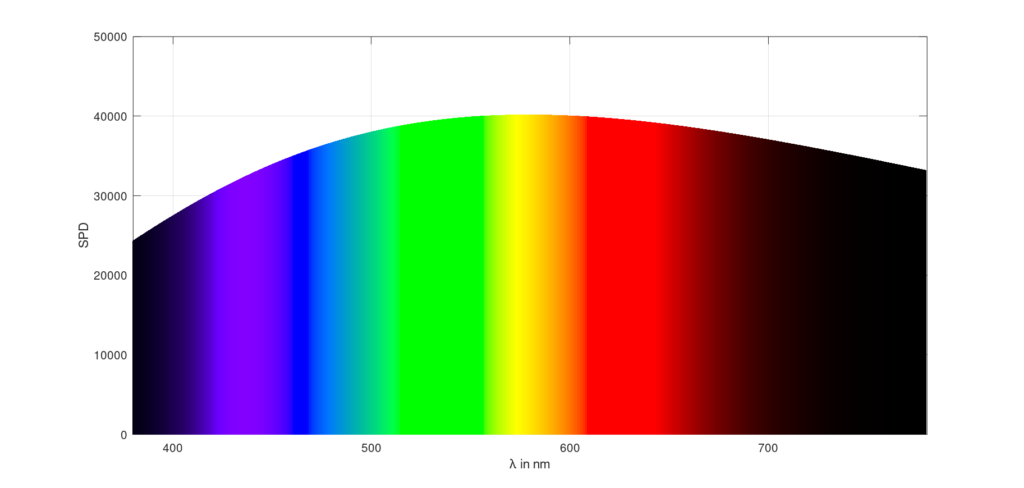
Spectral radiant exitance for several black body temperatures:
lam = 0:10:1000;
T = 4000:1000:9000;
M = planck(T,lam);
plot(lam,M)
xlabel('\lambda in nm')
ylabel('spectral radiant exitance in W m^{-2} nm^{-1}')
legend('4000 K','5000 K','6000 K','7000 K','8000 K','9000 K')
Result:
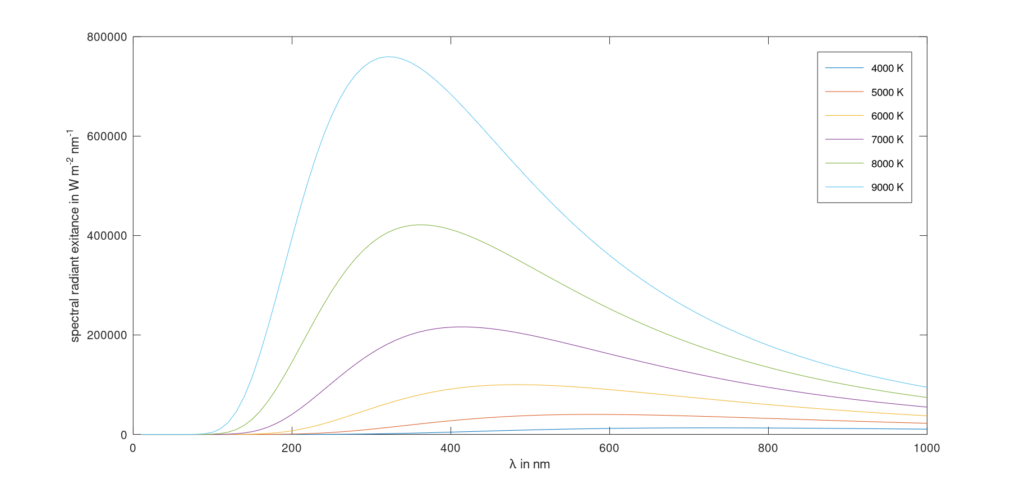
Colour coordinates for a planck radiator of 9000 K:
[~,x,y,u,v] = planck(9000)
Result:
x = 0.2869 y = 0.2956 u = 0.1921 v = 0.2969
Reference
Günther Wyszecki, W. S. Stiles: Colour Science – Concepts and Methods, Quantitative Data and Formulae, 2nd Edition. John Wiley & Sons, Inc., 2000, ISBN: 978-0-471-39918-6.
The NIST Reference on Constants, Units and Uncertainty, first radiation constant
The NIST Reference on Constants, Units and Uncertainty, second radiation constant