The ciesky function calculates the corresponding luminance distribution for a Tregenza hemisphere with 145 patches according to the CIE procedure described in ISO 15469. The resulting luminance distribution is relative to the zenith patch, but the function allows absolute values for horizontal illuminance E_{\text{h}} or zenith luminance L_{\text{Z}}.
L = ciesky(type,sunaz,sunel,'target',value,'mode',value)
Where:
| Parameter | Description |
L | Returns the luminance distribution of a Tregenza hemisphere, column-wise for multiple sky type input. |
type | Defines the CIE sky type 1 – 16. Multiple sky types can be submitted as vector. |
sunaz | Is the sun azimuth angle in ° (0 – 360). The azimuth angle starts in north position and goes clockwise. |
sunel | Is the sun eleavation angle in ° (0–90). |
'target' | Specifies the target unit (optional) ’Lz’ for zenith luminance ’Eh’ for horizontal illuminance |
target value | Absolute value of specified target: horizontal illuminance E_{\text{h}} or zenith luminance L_{\text{Z}} |
'mode' | Enables to specifies the luminance determination mode. (optional) |
mode value | ’center’ for luminance detmerination for the patch center ’mean’ for mean luminance of the 4 patchcorner luminances as suggested by Tregenza |
Examples
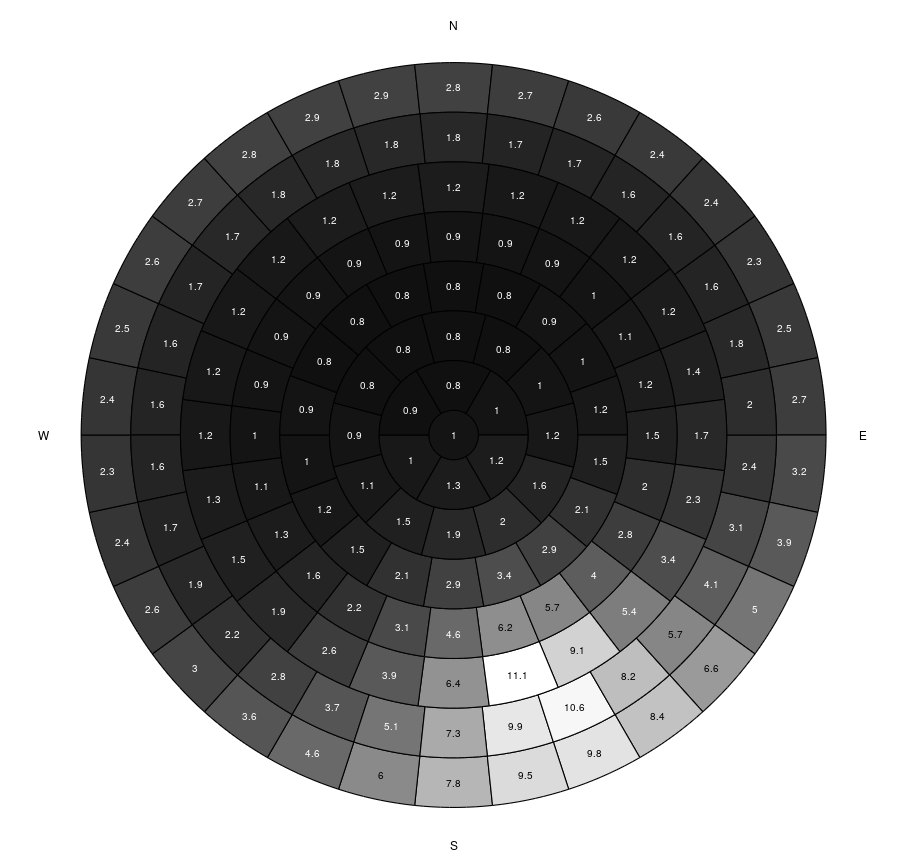
Relative luminance distribution for CIE clear sky type 12 at sun position \alpha = 160° and \gamma = 30°:
L = ciesky(12,160,30); plottregenza(L)
See also: plottregenza
Result:
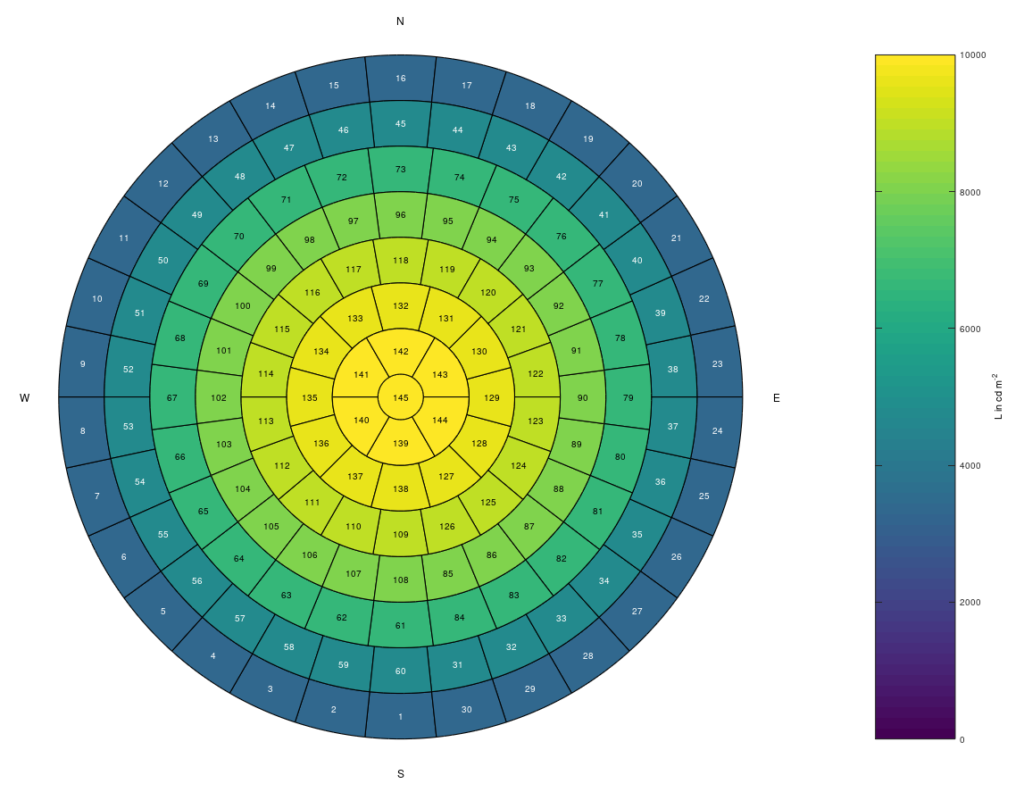
Absolute luminance distribution for CIE overcast sky type 1 at sun position \alpha = 210° and \gamma = 40° with a zenith luminance of L_{\text{Z}} = 10000~\text{cd}\,\text{m}^{-2} and Trgenza patch numbers:
L = ciesky(1,210,40,'Lz',10000);
p = 1:145;
plottregenza([p' L],'clr','L in cd m^{-2}')
See also: plottregenza
Result:
Absolute luminance distribution for CIE intermediate sky type 7 at sun position \alpha = 180° and \gamma = 20° with a resulting horizontal illuminance of E_{\text{h}} = 50000~\text{lx}:
L = ciesky(7,180,20,'Eh',50000);
plotskydirecto(L,'clr','L in cd m^{-2}')
% Test E_h
Eh = polardataE(L)
See also: plotskydirecto, polardata
Result:
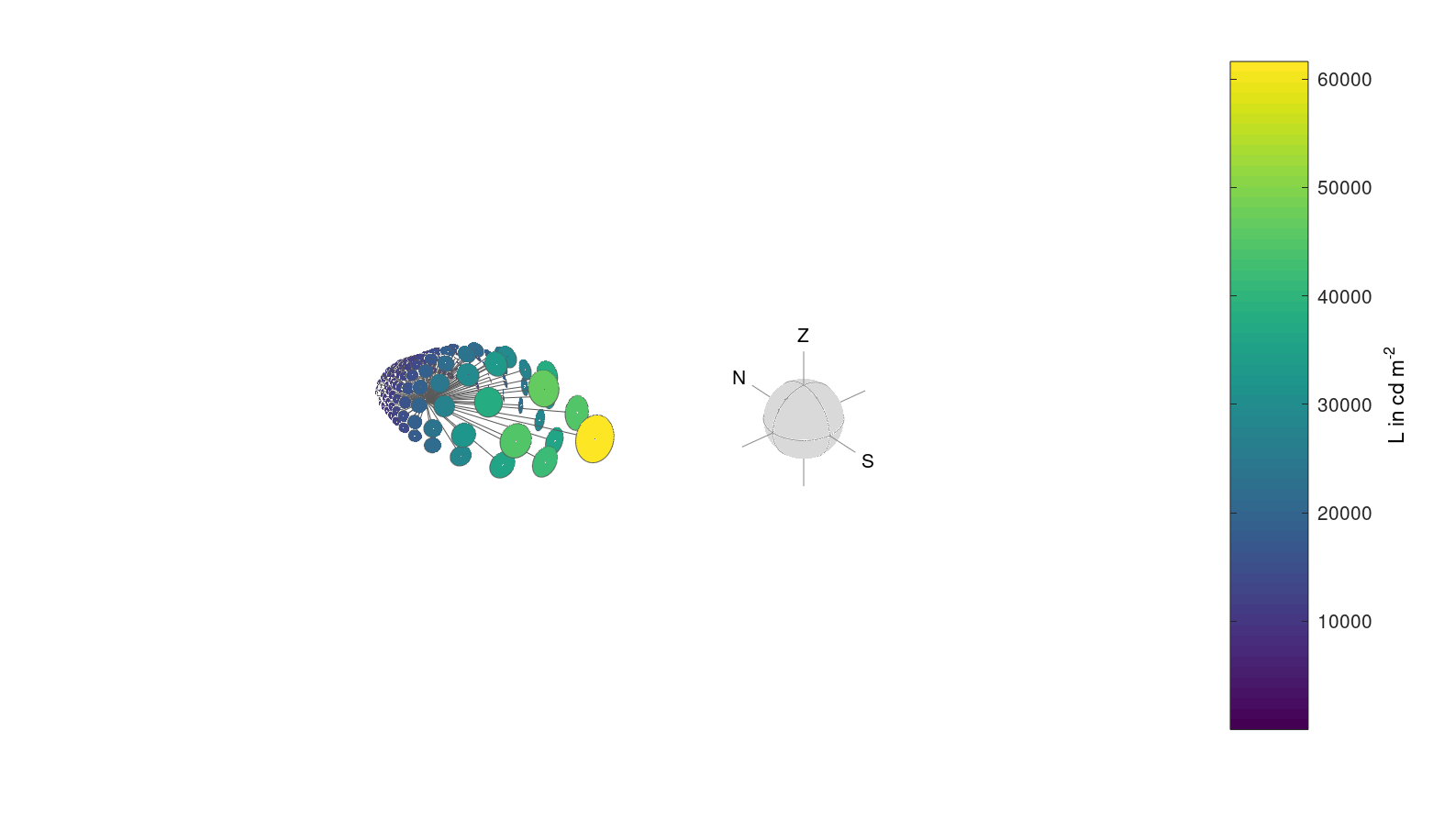
Eh = 5.0000e+04
Absolute radiance distribution for given uniform Correlated Colour Temperature (CCT) T_{\text{cp}} = 6500~\text{K} and resulting horizontal illuminance of E_{\text{h}} = 10000~\text{lx}:
% calculate relative luminance sky distribution: % CIE sky type 5 L = ciesky(5,180,60,'Eh',10000); % Judd CCT to spectrum calculation for Tcp = 6500 K [spec,lam] = ciecct2spec(6500); % repeat CCT spectrum 145 times spec = repmat(spec,145,1); % calculate luminance of CCT spectrum Y = ciespec2Y(lam,spec); % weight radiance distribution correctly spec = spec.*L./Y % test Eh = 10000 Eh = polardataE(ciespec2Y(lam,spec))
See also: ciecct2spec, ciespec2Y, polardataE, specsky
Result:
spec = 0.0000 0.0014 0.0028 ... 0.0000 0.0014 0.0028 ... 0.0000 0.0014 0.0028 ... 0.0000 0.0014 0.0028 ... 0.0000 0.0014 0.0028 ... . . . Eh = 1.0000e+04
References